Logic
Many people assume that they are rational simply because they have the ability to think. But reasoning well is not automatic—it requires skill, effort, and practice. In our daily lives, we are constantly presented with arguments, from political debates and advertisements to social media posts and personal conversations. Yet, without the ability to critically evaluate these arguments, we risk being misled by faulty reasoning, manipulated by persuasive rhetoric, or trapped in our own cognitive biases.
For this class meeting, we will be introduced to logical reasoning as a foundational tool for thinking clearly and critically. We will explore key concepts, such as validity and soundness, and we will learn to distinguish between arguments that are merely persuasive and those that are genuinely well-reasoned. We will also examine fundamental logical structures, including modus ponens and hypothetical syllogisms, as well as common fallacies that can undermine arguments. By developing a deeper understanding of these principles, we will strengthen our ability to evaluate claims, construct sound arguments, and engage more thoughtfully with the world around us.
Text: Tomas Bogardus, “The Foundations of Reasoning” See our Interactive Essay. For full text see the course packet.
Suggested reading: Plato’s “Allegory of the Cave” (The Republic, Book VII 514a-520a). Plato’s “Allegory of the Cave” is widely available. A free version is available here. This interactive version is recommended for the uninitiated.
Learning outcomes:
- Learn basic terminology.
- Distinguish between valid and sound arguments, and learn how to evaluate the logical structure of arguments.
- Identify modus ponens, modus tollens, and hypothetical syllogisms in everyday arguments.
- Recognize formal and informal logical fallacies and understand how they undermine arguments.
Do this:
- Do the practice problems on validity that are given to you in class.
Introduction
You have embarked on a course about the foundations of reasoning, and those foundations are arguments. No matter what you go on to do with your life, there will be arguments involved, from beginning to end, from top to bottom. But let me stop you right there: the word ‘argument’ is being used here in a special, technical sense. In life outside this classroom, many people use the word ‘argument’ to mean something like a heated, contentious, probably emotional dispute. Bickering, squabbling, quarrelling. But that’s not what we mean here by ‘argument’. Here, we mean an attempt to persuade someone of something, using reasons. In this class, we will give and receive arguments in a civil way, without any quarrelling.
So that’s what I mean when I say your life will involve arguments. I’d bet that before the end of the day today—even before the end of this paragraph!—someone will try to convince you of something. Maybe they’ll try to convince you to do something—like join their political movement—or maybe they’ll try to convince you to believe something, like that cricket protein is the way of the future. Whether you go on to practice law, or medicine, or go into business, or raise children, or produce great art—whatever you go on to do, you will be bombarded with arguments. Some will be good, but many will be bad. This class will prepare you to tell the difference.
In this class, we will learn how to identify arguments, to know when an argument is happening. We will also learn to clarify arguments, to lay them out step by step. And, perhaps most importantly, we will learn how to evaluate arguments, to see whether they’re good or bad, whether we should accept them or reject them. Since arguments are all around us, this class may well be the most useful class you will ever take. Becoming adept at finding, clarifying, and evaluating arguments will allow you to see through the flimsy arguments that we so often hear from the media, from politicians, and even from scientists. This training is a kind of intellectual self-defense; citizens trained in argument are not easily misled by charisma or by rhetoric. Instead, they have a taste for the truth and a talent for finding it. So, let’s get started!
Terminology
Proposition. A proposition is something that can be true or false. These are typically expressed by complete declarative sentences, but they are not merely sentences. “Es regnet” and “It’s raining” are two distinct sentences, but they ‘say the same thing’, they‘express the same thought’. The thing that is said, the thought that’s expressed, is a proposition, and it can be true or false.
Exercise: Think of some propositions. Some true, some false.
For example: Thomas Aquinas was a philosopher. Snow is whtie. California is in Florida.
Argument. An argument is composed of one premise, or several premises, together with a conclusion.
Premise. A premise is a proposition that, often together with other premises, is meant to support or prove a conclusion.
We use a variety of words to signal when we’re providing premises, when we’re giving reasons. For example: because; here’s why; for; since; after all. Can you think of any others?
Conclusion. A conclusion is a proposition that is meant to be supported or proven by premises.
We use a variety of words to signal when we’re drawing conclusions. For example: therefore; in conclusion; so; hence; thus; for all these reasons; that’s why. Can you think of any others?
Exercise: Think of some arguments. They needn't be profound.
For example, here's one: Some number of sharks existed long before any concepts existed. Therefore, numbers are not concepts.
We come next to probably the most important concept in this essay: entailment. I’m a professional philosopher, and I don’t think it’s an exaggeration to say that what I do for a living is try to spot entailment: when it’s present, and when it’s absent. I’d say that’s the most important skill that philosophy helps one to develop, and you’ll find it useful no matter your future path. Let’s first define entailment.
Entailment. To say that proposition P entails proposition Q is to say that, if P is true, then Q must be true. P guarantees the truth of Q. There’s absolutely no way around it; there are no possible exceptions.
If we gathered all the possible scenarios in which proposition P is true into a circle, and all the possible scenarios in which proposition Q is true into a circle, we could depict entailment like this:
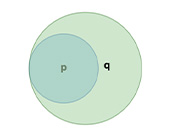
If P entails Q, then those scenarios in which P are true are a subset of the scenarios in which Q is true.
Let’s think of some examples of entailment, to help us understand the concept. Let the name ‘Joe’ refer to the nearest man with wet hair. What is entailed by this proposition?
P: Joe’s hair is wet.
You might be tempted to think P entails that Joe just took a shower. That may be probable, but it’s not guaranteed. After all, it may be that Joe’s hair is wet because he walked through the rain, or the sprinklers, or because he was in a water-balloon fight, or… Here are a few examples of propositions that are entailed by P, the proposition that Joe’s hair is wet:
Q: Joe has hair.
Q': Something is wet.
Q": Joe exists.
These propositions aren’t very interesting! But each one is absolutely guaranteed by the truth of proposition P. Hopefully, when you do more philosophy, you’ll find examples of entailment that are more profound.
Exercise. Pick a proposition at random. Think of propositions that are entailed by it. Make sure the truth of the first proposition absolutely guarantees the truth of the second proposition! Do that a few more times, first starting with a proposition that’s actually true, and then starting with a proposition that’s actually false.
Now that we understand entailment, let’s talk about how it applies to arguments. Something that we’re looking for in arguments is validity.
III. Valid and Sound Arguments
Validity. To say that an argument is valid is to say that its premises entail its conclusion.
Remember, entailment means an absolute guarantee of truth. If the premises of a valid argument are true, then the conclusion must be true. So, that’s how we check for validity. We suppose that the premises are true, and then ask ourselves whether the conclusion would have to be true, on that supposition. Of course, a valid argument may have premises that are actually true, but a valid argument also might have false premises. For example:
1. Max is a human.
2. So, Max is a mammal.
Do you see how this conclusion is guaranteed to be true, supposing that the premise is true? That’s why it’s a valid argument. And notice that it’s valid whether or not the premise is actually true, i.e. whether or not Max really is a human. Come to think of it, you don’t really know what the name ‘Max’ refers to. It might refer to a human, but it might also refer to, say, a dog, or an iguana. But that doesn’t matter for validity. For validity, we just ask ourselves: what if the premise(s) were true? Must the conclusion be true, in that case? And here, the answer is ‘yes’. Even if Max is an iguana, it’s still true that if Max is a human, then he must be a mammal. The ‘if’ is doing a lot of work!
Exercise. Think of some more valid arguments; they needn’t be profound. Try to find some with true premises and a true conclusion. Then find some with false premises and a false conclusion. Then find some with false premises and a true conclusion. Fact: you cannot find a valid argument with true premises and a false conclusion. Why is that?
For example:
Premise 1: All creatures that can fly are birds.
Premise 2: Penguins are birds.
Conclusion: Therefore, penguins can fly.
This argument is valid because the logical structure works perfectly - if both premises were true, the conclusion would necessarily follow. The form is:
- All A are B
- C is A
- Therefore, C is B
However, it's not sound because the first premise is false! Not all flying creatures are birds (think bats, insects, flying squirrels). So while the argument follows logical rules correctly, it leads to the obviously incorrect conclusion that penguins can fly.
Clearly, it’s much better for an argument to be valid than to be invalid. But the fact that valid arguments can have false premises should suggest to you that validity isn’t the whole story when it comes to good arguments. We’d like our arguments to be valid, but we’d also like them to have all true premises. That’s what we’re looking for in philosophy, that’s the goal: valid arguments with true premises. When that happens, the conclusion has to be true, and we say that the argument is sound.
Soundness. To say that an argument is sound is to say that it is valid, and all of its premises are true.
Soundness is the best case scenario, in which the argument is valid and the premises are true. Here's a similar example of an argument that is both valid and sound:
Premise 1: Plato was a human.
Premise 2: If someone was a human, then that person was a mammal.
Conclusion: So, Plato was a mammal.
This argument uses the same logical structure as the previous example:
- All A are B
- C is A
- Therefore, C is B
But unlike the previous example, this argument is sound because both premises are actually true:
- It is true that Plato was a human.
- It is true that all humans are mammals.
Since the argument is valid (follows logical rules) and both premises are true, the conclusion must be true as well. And indeed, Plato was a mammal!